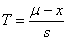En la generalidad de los casos, no disponemos de la desviación standard de la población, sino de una estimación calculada a partir de una muestra extraída de la misma y por lo tanto no podemos calcular Z.
donde S es la desviación standard muestral, calculada con n-1 grados de libertad.Nótese que utilizamos S, la Desviación Standard de una Muestra, en lugar de m, la Desviación Standard de la Población.El estadístico T tiene una distribución que se denomina distribución T de Student, que está tabulada para 1, 2, 3, ... etc. grados de libertad de la muestra con la cual se calculó la desviación standard.
La distribución T tiene en cuenta la incertidumbre en la estimación de la desviación standard de la población, porque en realidad la tabla de T contiene las distribuciones de probabilidades para distintos grados de libertad.La distribución T es mas ancha que la distribución normal tipificada Para un número de grados de libertad pequeño. Cuando los grados de libertad tienden a infinito, la distribución T tiende a coincidir con la distribución normal standard. Es decir, en la medida que aumentemos el número de observaciones de la muestra, la desviación standard calculada estará mas próxima a la desviación standard de la población y entonces la distribución T correspondiente se acerca a la distribución normal standard.
El uso de la distribución T presupone que la población con que estamos trabajando tiene una distribución normal.Distribución de Promedios MuestralesPara comprender que significa distribución de promedios muestrales, vamos a suponer que realizamos un experimento con bombos como los usados en la lotería. Colocamos un número muy grande de bolas blancas en un bombo blanco, en cada una de las cuales figura un dato X. Este bombo representa la población de observaciones X, y tiene media m y varianza s2. Supongamos que a continuación hacemos los siguiente:
1) Tomamos una muestra de n=10 bolas blancas.
2) Calculamos la media y la anotamos en una bola azul.
3) Colocamos la bola azul en un segundo bombo de color azul.
4) Devolvemos las bolas blancas a su bombo y le damos vueltas.
5)Repetimos toda la operación muchas veces hasta que el bombo azul esté lleno de bolas azules.
Aqui les dejo la tabla para poder operar. En el caso de quienes estudiamos en Universidad Galileo es la tabla A3 de su texto de Estadistica.